| Cohen’s kappa statistic ถ้าเป็นกรณีที่เป็นสถานการณ์ที่ Object ที่ไม่ได้ถูกจัดลำดับ แต่ถูกจัดลงกลุ่มต่างๆ ( categories ) เช่น ในกลุ่มนักจิตวิทยา k คนจัดผู้ป่วย N คน ในกลุ่มการรักษาต่างๆ ( treatment ) หรือในกลุ่มของชนิดของโรคจิต โดยนักจิตวิทยาแต่ละคนจะเป็นอิสระกัน และจัดผู้ป่วยแต่ละคนเป็นอิสระต่อกัน ในการจัดกลุ่มการรักษา ต้องการวัดว่านักจิตวิทยาทั้ง k คน มีความเห็นสอดคล้องกันหรือไม่ ในการจัดผู้ป่วยทั้ง N คนในการรักษาแบบต่างๆ (กลุ่มต่างๆ)
จะใช้สถิติที่เรียกว่า “Kappa statistic” หรือ Cohen's kappa statistic ซึ่งแนวความคิดจะคล้ายกับการมี 2 raters หรือ raters ประเมินแต่ pair of object ในหัวข้อที่ผ่านมา
วิธีการ
ถ้ามี N ตัวอย่าง ซึ่งจะถูกกำหนดให้อยู่ในกลุ่มใดกลุ่มหนึ่ง จาก m กลุ่มโดย m กลุ่มนี้จะมีลักษณะเป็น นามบัญญัติ จากกลุ่มของ k raters ข้อมูลที่ได้สามารถจัดลงตารางดังนี้

เมื่อ n ij = จำนวน Raters ที่กำหนดให้ Object ที่ i ลงในกลุ่มที่ j เนื่องจากแต่ละ Rater กำหนดให้แต่ละ Object ลงในกลุ่มใดๆ ดังนั้นผลรวมทาง row ต้องเท่ากับ k ในทุก row ส่วนผลรวมทางคอลัมน์จะเท่ากับ C j =  n ij n ij
ถ้า ผู้ประเมิณ มีความเห็นสอดคล้องกันอย่างสมบูรณ์ ค่าความถี่ n ij ในบางเซล ควรมีค่า = k และในเซลอื่นๆ (ใน row นั้น) จะมีค่าความถี่เท่ากับ 0 แต่ถ้าไม่มีความเห็นสอดคล้องกัน ค่าความถี่ในเซลต่างๆ (ใน row หนึ่งๆ) ควรมีค่าเป็นอย่างสุ่ม ( random )
ค่าสถิติ Kappa จะเป็นค่าอัตราส่วน ของความน่าจะเป็นที่คาดว่าจะเป็น เมื่อ H 0 (มีความเป็นอิสระกัน) เป็นจริง กับ ความน่าจะเป็นที่สูงสุด

เมื่อ P(A) = ค่าสัดส่วนที่ k Raters ที่มีความเห็นสอดคล้องกัน
P(E) = ค่าส่วนที่ k Raters ที่มีความเห็นสอดคล้องกันโดยบังเอิญ( by chance )
K = 1 ถ้ามีความเห็นสอดคล้องอย่างสมบูรณ์
K = 0 ถ้ามีความเห็นไม่สอดคล้องกัน ( No agreement among the raters ) 
ตัวอย่างที่ 2 การศึกษาเกี่ยวกับปลาตัวผู้ ในระหว่างการวางไข่ จะพบว่าปลาตัวผู้จะเปลี่ยนสีและสร้างอาราเขต สร้างรัง และมีความก้าวร้าว ให้นักวิจัย 4 คน สังเกตปลา 29 ตัว ว่าเปลี่ยนสีไปในกลุ่มต่างๆ 5 ระดับ น้อยมากถึง มากที่สุดได้ข้อมูลดังนี้




มีความสอดคล้องกันในระดับปานกลางของนักวิจัย 4 คน
การทดสอบนัยสำคัญของค่า K
การหาหารแจกแจงค่า K กรณี N เล็ก จะยุ่งยาก ดังนั้นจะใช้การประมาณด้วยการแจกแจงปกติ เมื่อ N ใหญ่ โดย 

Z วิกฤต = 2.32 ตกใน CR. ปฏิเสธ 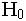 ยอมรับ ยอมรับ  ยอมรับ H 1 นั่นคือ นักวิจัย 4 คนมีความเห็นสอดคล้องกัน ยอมรับ H 1 นั่นคือ นักวิจัย 4 คนมีความเห็นสอดคล้องกัน
นอกจากนี้ ยังอาจวัดค่า Kappa ได้อีก แบบหนึ่ง จาก ผู้ประเมิน 2 คน ดังนี้
ตารางข้อมูลตัวอย่าง จะเป็นดังนี้ 
ความถี่ในเซลต่างๆ คือ จำนวนครั้งที่ Rater ที่ 1 และ2 มีความเห็นเหมือนกันในการจัดกลุ่มลงในกลุ่มย่อย หนึ่งๆ เช่น ความเห็นของจิตแพทย์2 คน (Psychiatrist) ที่จำนวนคนไข้กลุ่มหน้าใน 3 กลุ่ม คือ
Endogenous depression; ED Reactive depression; RD
Obsessional neurosis; ON

หมายความว่าจิตแพทย์ทั้ง 2 มีความเห็นสอดคล้องกันอย่างสมบูรณ์
การจัดกลุ่มทาง row และ column แม้จะไม่มีลักษณะเป็นลำดับที่ของกลุ่ม (Ordinal Scale) แต่ควรจัดให้เหมือนกันทั้งทาง row และ column (คือถ้าจัดจาก ED RD และ ON ทาง row ก็ควรจะจัดเช่นนี้ทาง column (และอาจสลับที่กลุ่มย่อยแบบใดๆก็ได้ แต่ทาง row และ column ควรจัดเหมือนกัน)

ซึ่งแสดงถึง ความสอดคล้องกันอย่างสมบูรณ์
หลักการนี้ นอกจากจะใช้วัดความสอดคล้องของ 2 ผู้ประเมิน แล้วยังอาจใช้วัด Reliability ของ 2 test ซึ่งวัดจากหน่วยทดลอง n สิ่ง โดยจัดลงในกลุ่มย่อยต่างๆ
ตัวอย่างที่ 3 Pathologist 2 ท่าน คือ X และ Y ได้จำแนก 118 slides เพื่อแสดงถึงการมี carcinoma of the uterine cervise อย่างเป็นอิสระโดยผลจำแนกเป็น 4 ระดับ คือ
1. Nagative
2. atypical aquamous hyperplasia
3. carcinoma in situ
4. aquamous or invasive carcinoma
ได้ข้อมูลดังตารางต่อไปนี้

สรุป ค่า Kappa ต้องใช้กับข้อมูลที่เป็น Nominal ไม่ใช่ Ordinal แต่ค่า Kappa ยังมีข้อด้อยคือ จากตารางบางชนิด อาจคำนวณได้ค่า Kappa เป็นลบได้ ในกรณีนี้การหาค่า Kappa เพียงอย่างเดียว อาจจะไม่เพียงพอที่จะอธิบายถึงความสอดคล้อง จำเป็นต้องศึกษาในขั้นสูงต่อไป เช่น การสร้างโมเดลแสดงความสอดคล้องกัน โปรแกรมคำนวณ 2 Raters โปรแกรมคำนวณ k Raters
_____________________________________________ <<หน้าก่อนหน้า |
