การทดสอบของครัสคาลและวัลลิส (The Kruskal-wallis One-Way Analysis of Variance By Rank Test)

      ใช้ทดสอบว่า ประชากร k กลุ่มมีค่ามัธยฐานเท่ากันหรือไม่ โดยมีวิธีกรที่สำคัญคือ ค่าคาดหมายของลำดับที่ของข้อมูลตัวอย่างแต่ละกลุ่ม ควรมีค่าพอๆกัน ข้อมูลที่นำมาทดสอบประกอบด้วยข้อมูลจากตัวอย่างสุ่ม k ชุด แต่ละชุดอาจมีขนาดตัวอย่างแตกต่างกัน ข้อมูลที่จะใช้วิเคราะห์ต้องมีมาตราวัดอย่างน้อยเป็นแบบเรียงลำดับ ( Ordinal Scale ) และมีการแจกแจงแบบต่อเนื่อง

การทดสอบนี้นิยมใช้แทนการทดสอบแบบเอฟ ( F-test ) ในสถิติที่ใช้พารามิเตอร์ในกรณีที่ข้อกำหนดเบื้องต้นของการทดสอบเอฟ ไม่เป็นจริง

สมมติฐาน

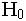: ค่ามัธยฐานของประชากร k กลุ่มไม่แตกต่างกัน
: ค่ามัธยฐานของประชากรอย่างน้อย 1 คู่ แตกต่างกัน

ตัวอย่างที่ 3.11 กำหนดให้มีวิธีการสอน 3 วิธีคือ ก ข และ ค นำไปใช้สอนวิชาคณิตศาสตร์ให้กับนักศึกษาจากตัวอย่างนักศึกษาที่มีพื้นฐานความรู้ใกล้เคียงกันทั้งหมด 13 คน ถูกสุ่มให้เรียนด้วยวิธีทั้ง 3 ด้วยจำนวน4 , 4 และ 5 คนตามลำดับ หลังจากเวลาผ่านไปพอสมควร ทำการทดสอบได้ผลดังนี้

ต้องการเปรียบเทียบวิธีการสอนทั้ง 3 วิธี ว่าจะให้ผลแตกต่างกันหรือไม่ ที่ระดับนัยสำคัญ 0.05

วิธีทำ จะ เลือกใช้วิธีทดสอบของ kruskal – Wallis เนื่องจากเป็นตัวอย่าง 3 กลุ่มที่เป็นอิสระกันและข้อมูลมีมาตราวัดเป็นแบบอันตรภาค วิธีการทดสอบทำได้ ดังนี้

1.จัดลำดับของข้อมูลที่นำมารวมเป็นชุดเดียวกัน โดยจัดลำดับจากน้อยไปหามากได้ข้อมูลลำดับ ดังนี้

ตัวอย่าง 3.12 ในการพิจารณากลุ่มอาชีพ 4 ประเภท เพื่อศึกษาระดับการครองชีพ (ซึ่งคิดจากการมีของใช้ชนิดต่างๆภายในบ้าน) ว่าแตกต่างกันหรือไม่ จึงสุ่มตัวอย่างคนจากอาชีพดังกล่าวมา 9 , 7 , 8 , และ 7 คนตามลำดับบันทึกคะแนนซึ่งคิดจากการมีของใช้ชนิดต่างๆ ภายในบ้านได้ข้อมูล X ij ดังตารางต่อไปนี้

      ในกรณีที่ค่าข้อมูลใน k กลุ่มอิสระกันนั้น มีค่าซ้ำกันมาก อาจจะซ้ำกันภายในกลุ่ม หรือ ระหว่างกลุ่มก็ได้ เช่นมีข้อมูลดังนี้

      จากวิทยาลัย 3 แห่ง สุ่มตัวอย่างคณาจารย์ เพื่อประเมินการบริหารงานของผู้บริหาร ใน 5 ระดับคือ แย่ที่สุด ปานกลาง ดี ดีมาก ยอดเยี่ยม โดยให้มีค่าคะแนน คือ 1 – 5 ตามลำดับ ถ้าได้ข้อมูลด้วยขนาดตัวอย่างจาก 3 วิทยาลัย คือ 15, 10, และ 12 ดังนี้