การทดสอบของวิลคอกซัน แมนท์วิทนีย์ ( The Wilcoxon-Mann-Whitney Test or The Wilcoxon Rank Sum Test )

      บางครั้งเรียกว่า Mann-Whitney U test หรือ Mann-Whitney- Wilcoxon test โดย Wilcoxon ได้ศึกษากรณีใช้ผลรวมลำดับที่ (rank sum) เป็นตัวสถิติทดสอบโดยที่ Mann และ Whitney ได้ชี้ถึงความสัมพันธ์ระหว่างตัวสถิติทดสอบที่เขาตั้งขึ้นกับของ Wilcoxon การทดสอบนี้นับได้ว่าเป็นการทดสอบที่มีประสิทธิภาพมากที่สุด มักนิยมใช้เพื่อเลี่ยงการใช้การทดสอบแบบที่ ในสถิติที่ใช้พารามิเตอร์ หรือเมื่อข้อมูลมีมาตราวัดต่ำกว่าแบบอันตรภาค

ข้อกำหนดเบื้องต้น

1. ข้อมูลประกอบด้วยตัวอย่างสุ่มด้วยค่า X 1 , X 2 …X n1 จากประชากรที่ 1 และตัวอย่างสุ่มอีก 1 ชุด ด้วยค่าสังเกต Y 1 , Y 2 …Y n2 จากประชากรที่ 2 ซึ่งเป็นอิสระกัน

2. ตัวอย่าง 2 ชุดนี้เป็นอิสระกัน

3.ค่าตัวแปรสุ่มมีค่าต่อเนื่อง ( continuous )

4.มาตรวัดอย่างน้อยเป็นแบบเรียงลำดับ ( ordinal scale )

5. ฟังก์ชันการแจกแจง ของ 2ประชากร ต่างกันเฉพาะค่ากลาง (ซึ่งนิยมวัดด้วยมัธยฐาน , M x , M y ) นั่นคือ ประชากรทั้ง 2 ต้องมี การแจกแจงที่เหมือนกัน ต่างกันเฉพาะค่ากลางเท่านั้น เช่น สมมติว่าประชากรทั้ง 2 มีการแจกแจงปกติ ดังนั้น อาจเขียนรูปโค้งการแจกแจง ดังนี้

สถิติที่ใช้ทดสอบ ในที่นี้จะเสนอวิธีการของ wilcoxon (1945) และ Mann, Whitney (1947) ซึ่งต่างก็เสนอวิธีการทดสอบของตนเอง และในที่สุดสามารถหาความสัมพันธ์ของทั้ง 2วิธีดังต่อไปนี้

      1.วิธีการของ wilcoxon ได้ใช้แนวคิดคล้ายการทดสอบของ wilcoxon signed Rank test คือใช้ผลรวมของลำดับที่ ( sum of rank or rank sum ) ของตัวอย่างชุดหนึ่งในข้อมูลรวมทั้งหมด ( n 1 +n 2 จำนวน) ที่ได้เรียงลำดับจากน้อยไปหามาก โดยคาดว่าถ้า 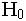เป็นจริง ในข้อมูลรวมทั้งหมดนั้นค่าลำดับที่ของตัวอย่างชุดหนึ่งควรจะมีคละกันไปทั้งค่าน้อย ปานกลาง และมาก ซึ่งจะทำให้ได้ผลรวมลำดับที่ ค่าหนึ่งที่ไม่มากเกินไปหรือน้อยเกินไป แต่ถ้า เป็นจริง ค่าผลรวมของลำดับที่จากตัวอย่างชุดหนึ่งจะมีค่ามาก หรือน้อยเกินไปดังตัวอย่างต่อไปนี้

ถ้ามีตัวอย่างสุ่มขนาด 4 ด้วยค่าตัวแปรสุ่ม X และอีกชุดหนึ่งด้วยขนาด 5 ด้วยตัวแปรสุ่ม Y ปรากฏว่าเมื่อนำทั้ง 9 จำนวนรวมกัน และเรียงลำดับ

      Wilcoxon ได้สร้างตารางแสดงค่าความน่าจะเป็นของค่า S ที่น้อยหรือมากเกินไปนี้ ซึ่งสามารถใช้ตารางดังกล่าวหาค่า p – value เพื่อตัดสินใจยอมรับ H 0 หรือปฏิเสธ H 0 ได้ แต่เนื่องจากค่า S ที่เล็กที่สุดจะแตกต่างกันไปตามขนาดตัวอย่างที่สุ่มมา จึงทำให้การสร้างตารางยากขึ้น และค่อนข้างใหญ่ ทำให้ไม่สะดวกในการใช้ ในที่นี้จึงไม่เสนอวิธีการของ Wilcoxon โดยตรงนี้ แต่จะปรับสูตรสถิติที่ใช้ทดสอบให้สัมพันธ์กับค่า S นี้ และสอดคล้องกับวิธีของ Mann, Whitney ซึ่งจะได้เสนอในลำดับต่อไป

ในกรณีตัวอย่างขนาดใหญ่ สามารถประมาณการแจกแจงของ S ด้วยการแจกแจงปกติ ดังสูตร

      2. วิธีการของ Mann, Whitney มักเรียกชื่อการทดสอบ ของเขาทั้งสองว่า Mann-Whitney U test ซึ่งกำหนดให้ตัวสถิติ U คือ การนับจำนวนค่าสังเกตในตัวอย่างชุดหนึ่งที่นำหน้า ( exceeding ) แต่ละค่าสังเกตในตัวอย่างอีกชุดหนึ่งในข้อมูลที่นำมารวมกันและเรียงลำดับ การคำนวณหาค่า U สามารถทำได้ง่ายไม่จำเป็นต้องใช้คอมพิวเตอร์ และวิธีการนี้ยังเป็นพื้นฐานในการหาช่วงความเชื่อมั่นของผลต่างค่ามัธยฐานใน 2 ประชากรด้วย

      3.วิธีการของ wilcoxon และ Mann-Whitney Mann-Whitney ได้แสดงความสัมพันธ์ระหว่างสถิติทีใช้ทดสอบของเขากับของ wilcoxon พบว่า

ตัวอย่างที่ 3.9 เพื่อทดสอบความแข็งของเหล็กที่ได้จาก 2 แหล่ง คือ A และ B ได้สุ่มตัวอย่างเหล็กจากแหล่ง A มา 4 ชิ้น และจากแหล่ง B มา 5 ชิ้น แล้วนำ 2 ชิ้นมาขัดถูกัน พิจารณาดูว่าชิ้นใดมีร่องรอยเสียหายมากกว่า ให้เป็นชิ้นที่มีความแข็งน้อยกว่า ทำเช่นนี้กับตัวอย่างทั้ง 9 ชิ้น แล้วให้ลำดับที่ 1 แก่ชิ้นที่แข็งน้อยที่สุด จนถึงอันดับที่ 9 คือชิ้นที่แข็งที่สุด

ได้ข้อมูลผลการทดลองดังนี้ A A A B A B B B B

ลำดับที่ 1 2 3 4 5 6 7 8 9

จงทดสอบสมมติฐานว่า เหล็กจากแหล่งทั้ง 2 มีความแข็งไม่แตกต่างกันที่ระดับนัยสำคัญ 0.05

วิธีทำ ใช้การทดสอบของ wilcoxon และ Mann Whitney เนื่องจากเป็นกรณี 2 กลุ่มตัวอย่างที่เป็นอิสระกัน และมีมาตรวัดข้อมูลแบบเรียงลำดับ พิจารณาในแง่ค่ากลาง คือ

      การทดสอบของ wilcoxon- Man- Whitney แบบมีซ้ำมาก (The wilcoxon – Man – Whitney Test with ties)

ถ้าค่าข้อมูลที่เป็นลำดับที่ในกลุ่มใดๆ 2 กลุ่มนั้นมีค่า ซ้ำกันมาก อาจจัดข้อมูลใหม่เป็น ตารางแจกแจง 2 ทาง โดยแถวนอนมี 2 แถว หมายถึง 2 กลุ่มตัวอย่างที่อิสระกัน และแถวตั้งจัดเป็นค่าลำดับที่ และนับความถี่ลงเซลต่างๆ ซึ่งตารางนี้จะมีลักษณะแบบเรียงลำดับทางแถวตั้ง อาจเรียกชื่อว่าเป็น Singly ordered contingency table เช่นมีข้อมูลดังต่อไปนี้

สุ่มตัวอย่างคนไข้ 4 คน ให้ใช้ยา A และคนไข้ 3 คนใช้ยา B หลังจากเวลาผ่านไประยะหนึ่ง ประเมินผลการรักษา โดยให้ แพทย์ประเมินในระดับความพอใจ จาก 1 – 3 (1 น้อยที่สุด) ได้ข้อมูลดังนี้

จะพบว่าค่าข้อมูลซึ่งมีค่า 1 – 3 มีค่าซ้ำกันมาก การให้ลำดับที่ต้องใช้ค่าเฉลี่ย ของลำดับที่ โดย

ค่า 1 มีสองค่า ได้ลำดับที่เฉลี่ยของลำดับ 1 และ 2 คือ 1.5

ค่า 2 มีสามค่า ได้ลำดับที่เฉลี่ยของลำดับ 3 , 4 และ 5 คือ 4

ค่า 3 มีสองค่า ได้ลำดับที่เฉลี่ยของลำดับ 6 และ 7 คือ 6.5

จะวิเคราะห์ข้อมูลแบบตารางที่เรียกว่า Singly ordered contingency table ด้วยสถิติ wilcoxon – Man – Whitney แบบปรับ ties ดังนี้

จัดข้อมูลลงตารางการณ์จร 2 ทาง และบันทึกความถี่ จะได้ตารางการณ์จรดังนี้

ถ้าพิจารณาตารางใหม่นี้ จะพบว่าสามารถใช้สถิติ วิเคราะห์ได้ เพราะเป็นตารางการณ์จร แต่เนื่องจากขนาดตัวอย่างเล็กมาก รวมทั้งความถี่คาดหวังจะมีค่าน้อยกว่า 5 มากเกิน 20 % ของจำนวนเซลทั้งทั้งหมด การใช้ จึงไม่เหมาะสม (ได้ค่า p – value = 0.31 ซึ่งก็ไม่พบนัยสำคัญระหว่างยาทั้งสอง)

เราสามารถใช้สถิติทดสอบของ wilcoxon – Man – Whitney แบบมี ties มากๆ ดังนี้