| ตารางชนิด rxk
เช่นเดียวกับหัวข้อ 3.1 คือ จะกล่าวถึงค่าสถิติที่ใช้วัดความสัมพันธ์ หรือเรียกว่าสัมประสิทธ์สหสัมพันธ์ ( Correlation coefficient ) แบบต่างๆ ก่อน และตอนท้ายจะกล่าวถึงสถิติทดสอบความเป็นอิสระ ดังนี้
ค่าสัมประสิทธิ์คาร์เมอร์ ( The Cramer coefficient )
ค่าสถิติคาร์เมอร์ จะใช้วัดความสัมพันธ์ของคุณลักษณะหรือตัวแปรที่มีลักษณะเป็นกลุ่ม ( Nominal scale ) โดยอาจมีค่าคงที่เดิมไม่ว่าการจัดตารางจะใช้แถวนอนและแถวตั้งเป็นคุณลักษณะใด และอาศัยการวัดจากพื้นฐานของสถิติทดสอบความเป็นอิสระของ  ดังนี้ ดังนี้

ตัวอย่าง 3.7 สุ่มตัวอย่างจากรายงานทางเศรษฐกิจของรัฐเซาท์คาโรไรนา ปี 1972 ซึ่งแสดงข้อมูลจากการสำมะโม( census ) ในปี 1970 เกี่ยวกับผู้อาศัยอยู่ในรัฐซึ่งมีอายุอย่างน้อย 25 ปีขึ้นไปในขณะนั้นโดยสนใจตัวแปรเพศ และจำนวนปีที่เข้ารับการศึกษา ได้ข้อมูลตัวอย่างดังตารางต่อไปนี้ จงวัดความสัมพันธ์ พร้อมทั้งทดสอบนัยสำคัญ ที่ระดับนัยสำคัญ .05


ข้อจำกัดของค่าสัมประสิทธิ์คาร์เมอร์ • ค่าสัมประสิทธิ์คาร์เมอร์ จะมีค่าเป็น 0 เมื่อตัวแปรทั้ง 2 ไม่มีความสัมพันธ์กันซึ่งคุณสมบัติข้อนี้ คล้ายสัมประสิทธิ์สหสัมพันธ์อื่นๆ เมื่อไม่มีความสัมพันธ์กันอย่างสมบูรณ์ ค่าสัมประสิทธิ์ควรจะมีค่าเป็น 0
• ค่าสัมประสิทธิ์คาร์เมอร์ ที่มีค่าเท่ากับ 1 ไม่ได้หมายความว่าตัวแปรทั้ง 2มีความสัมพันธ์กันอย่างสมบูรณ์ ซึ่งต่างจากค่าสัมประสิทธิ์สหสัมพันธ์ทั่วๆไป ที่มีความหมายว่าตัวแปรทั้ง 2 มีความสัมพันธ์กันอย่างสมบูรณ์ ค่าสัมประสิทธิ์คาร์เมอร์เท่ากับ 1 จะหมายถึงตัวแปรทั้ง 2 มีความสัมพันธ์กันอย่างสมบูรณ์ เฉพาะกรณีที่ตารางการจรณ์เป็นชนิด r = k และตาราง การณ์จรนี้ จะต้องมีแต่ละแถวนอน และแต่ละแถวตั้ง มีเพียงเซลเดียว ( single cell ) ที่มีค่าความถี่ไม่เป็น 0 ดังนั้นจะแสดงตัวอย่างเมื่อตารางการณ์จรเป็นชนิด r = k และ c 2 = 1 ดังนี้
จากการสุ่มตัวอย่างสุนัขมา 50 ตัวจาก 3 พันธุ์ และแยกตามขนาดจะได้ข้อมูลดังตารางต่อไปนี้
| พันธุ์ |
ขนาดสุนัข |
รวม |
ใหญ่ |
กลาง |
เล็ก |
| อัลเซเซียน |
20 |
0 |
0 |
20 |
| บลูด๊อก |
0 |
10 |
0 |
10 |
| เทอร์เรีย |
0 |
0 |
20 |
20 |
| รวม |
20 |
10 |
20 |
50 |
คำนวณได้ค่า ? 2 = 100 และ C 2 = 1 หมายความว่าตัวแปรพันธุ์ และขนาดสุนัขมีความสัมพันธ์กันอย่างสมบูรณ์ ในสองทิศทาง คือถ้าทราบตัวแปรหนึ่งจะทำนายหรือคาดคะเนค่า ตัวแปรที่เหลือได้ เช่น ทราบว่าเป็นสุนัขพันธุ์เทอร์เรีย ก็บอกได้ว่ามีขนาดเล็ก หรือแปลความกลับกัน ในกรณีตารางการจรณ์ชนิดใดๆ ที่ r ? k ค่าสัมประสิทธิ์คาร์เมอร์อาจจะมีค่า = 1 โดยมีความหมายว่ามีความสัมพันธ์ระหว่าง 2 ตัวแปรอย่างสมบูรณ์ แต่ในทิศทางเดียวกันเท่านั้น ( only one direction ) เช่น ในกรณีที่ r < k และสัมประสิทธ์มีค่า = 1 จะมีเพียงหนึ่งเซลทีมีควาถี่ไม่เป็น 0 ในแต่ละแถวตั้ง แต่จะต้องมีบางแถวนอน ( some rows ) ที่มีมากกว่าหนึ่งเซลที่มีความถี่ไม่เป็นศูนย์ (จะมี k – r เซลที่มีความถี่ไม่เป็นศูนย์) ดังนี้ ในกรณีนี้จึงมีความสัมพันธ์กันอย่างสมบูรณ์ จากตัวแปรทางแถวตั้ง ไปสู่ตัวแปรทางแถวนอนแต่จะไม่มีความสัมพันธ์อย่างสมบูรณ์จากตัวแปรทางแถวนอนไปสู่ตัวแปรทางแถวตั้ง และความสัมพันธ์จะมีทิศทางตรงข้ามกับที่กล่าวข้างต้น เมื่อค่าสัมประสิทธิ์ = 1 และ r > k ดังจะแสดงตารางชนิด r x k ที่คำนวณค่า C 2 = 1 ดังนี้
| อาชีพ |
เพศ |
พยาบาล |
นักบิน |
ประชาสัมพันธ์ |
รวม |
หญิง |
50 |
0 |
30 |
80 |
ชาย |
0 |
20 |
0 |
20 |
รวม |
50 |
20 |
30 |
100 |
แปลผลได้ว่า เมื่อทราบตัวแปรทางแถวตั้ง คือ อาชีพ เช่น นักบิน ก็พอจะทำนายได้ว่า ต้องเป็นเพศชาย (แถวนอน)หรือ
อาชีพ |
เพศ |
รวม |
| หญิง |
ชาย |
|
| พยาบาล |
50 |
0 |
50 |
นักบิน |
0 |
20 |
20 |
| ประชาสัมพันธ์ |
30 |
0 |
30 |
รวม |
80 |
20 |
100 |
สรุปได้ว่าในกรณีที่ค่าสัมประสิทธิ์ = 1 เมื่อ r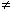 k ความสัมพันธ์จะมีลัษณะเป็นแบบสมบูรณ์ชนิดไม่สมมาตร ( asymmetrical perfect relation ) กล่าวคือ มีความสัมพันธ์อย่างสมบูรณ์เพียงทิศทางเดียวแต่ไม่เป็นทั้งสองทิศทาง k ความสัมพันธ์จะมีลัษณะเป็นแบบสมบูรณ์ชนิดไม่สมมาตร ( asymmetrical perfect relation ) กล่าวคือ มีความสัมพันธ์อย่างสมบูรณ์เพียงทิศทางเดียวแต่ไม่เป็นทั้งสองทิศทาง
• การหาค่าสัมประสิทธิ์คาร์เมอร์ได้ ต้องมาจากการใช้การทดสอบของ ดังนั้น ข้อจำกัดของ ดังนั้น ข้อจำกัดของ ควรจะเป็นจริง คือ ขนาดตัวอย่างต้องมีขนาดใหญ่ (เพื่อไม่ให้เกิดกรณีที่จะมีมากกว่า 20 เปอร์เซนต์ของจำนวนเซลทั้งหมด มีความถี่คาดหวังน้อยกว่า 5) ควรจะเป็นจริง คือ ขนาดตัวอย่างต้องมีขนาดใหญ่ (เพื่อไม่ให้เกิดกรณีที่จะมีมากกว่า 20 เปอร์เซนต์ของจำนวนเซลทั้งหมด มีความถี่คาดหวังน้อยกว่า 5)
• ค่าสัมประสิทธิ์คาร์เมอร์ ไม่สามารถนำไปเปรียบเทียบกับค่าสัมประสิทธ์อื่นๆ ได้ เช่น สัมประสิทธ์ของเพียร์สัน (ยกเว้นกรณีเป็นตารางชนิด 2x2 ) หรือสัมประสิทธ์ของสเปียร์แมนและเคนดอลล์
แม้จะมีข้อจำกัดดังกล่าวของค่าสัมประสิทธิ์คาร์เมอร์ แต่จะพบว่าค่าสัมประสิทธ์นี้มีข้อดีหลายประการคือ
• มีค่าสูงสุด = 1 ในขณะที่ค่า C มีค่าสูงสุดไม่เท่ากับ 1 แม้ว่าความหมายของการที่ค่าสัมประสิทธิ์ = 1 จะไม่มีความหมายถึงความสัมพันธ์อย่างสมบูรณ์เหมือนกันกับค่าสัมประสิทธิ์อื่นๆดังกล่าวในข้อ 2 ของข้อจำกัดแล้ว
• สามารถเปรียบเทียบค่าสัมประสิทธิ์คาร์เมอร์ ในกรณีตารางแจกแจงสองทาง r x k ใดๆได้
ความคิดพื้นฐานเกี่ยวกับสถิติประเภท PRE
โดยทั่วๆไปข้อมูลในตาราง ซึ่งจะก่อให้เกิดความสัมพันธ์ (มีความถี่เฉพาะช่องที่อยู่บนเส้นทแยง นอกเส้นทแยงเป็น 0 หมด) ไม่ค่อยปรากฏบ่อย ทั้งนี้เพราะมีปัจจัยอื่นๆนอกเหนือไปจากตัวแปรอิสระ ซึ่งไม่ได้บรรจุเอาไว้ในตารางมากระทบต่อตัวแปรตาม จึงมักพบแต่เพียงตารางข้อมูลที่มีความสัมพันธ์ระหว่างตัวแปรเป็นขนาดกลางๆ หรือขนาดมาก แต่ไม่ถึงขั้นสมบูรณ์ ด้วยเหตุนี้การตีความจึงมีความสำคัญ
สมมติว่ามีตารางข้อมูล ซึ่งถูกดัดแปลงให้เป็นค่า Probability เราเรียก joint probability distribution (A j , B k ) ดังนี้
ข้อมูลที่ถูกดัดแปลงเป็นค่า probability แล้ว
|
A1 |
A2 |
รวม |
B1 |
.20 |
.15 |
.35 |
B2 |
.10 |
.30 |
.40 |
B3 |
.10 |
.15 |
.25 |
รวม |
.40 |
.60 |
1.0 |
นั่นคือถ้า P (A j , B k ) คือ P(A 1 , B 1 ) ก็จะมีค่า probability = 0.20 หรือ P(A 2 , B 1 ) = 0.15 เป็นต้น
สมมติว่ามีการสุ่มเอาหน่วยใดหน่วยหนึ่งออกมาจากตารางนี้ โดยที่เราไม่ทราบเลยว่ามาจากช่วงใดของ A แล้วถามว่า หน่วยนี้มาจากช่วงใดของ B คำตอบก็ควรจะเป็น B 2 ทั้งนี้เพราะ B 2 มีผลรวมที่ใหญ่ที่สุด คือ 0.40 โอกาสที่จะเกิดช่วง B 2 จึงมากที่สุด แต่ก็เป็นไปได้ที่หน่วยที่สุ่มออกมานั้น ตามความเป็นจริงแล้วอาจมาจากช่วง B 1 หรือ B 3 ก็ได้ ดังนั้นจึงเกิดความผิดพลาดในการทำนาย = 0.35+0.25 = 0.60
การทำนายเช่นนี้และวิธีการหาค่าความผิดพลาดดังข้างต้น เป็นการใช้ประโยชน์จากค่า probability ที่ผลรวมของตัวแปรตามแต่เพียงอย่างเดียว
คราวนี้สมมติใหม่ว่าหน่วยที่ถูกสุ่มมานั้นทราบว่ามาจากช่วง A 1 ดังนั้นจึงควรทำนายว่าหน่วยนี้ควรมาจาก B 1 เพราะช่อง A 1 B 1 มีค่า probability ที่ใหญ่ที่สุดคือ 0.20 นั่นคือ probability ในการเดาถูกคิดจากเฉพาะช่วง A 1 เท่านั้นจะเท่ากับ 0.20/0.40 = 50% หรือคิดได้อีกวิธีหนึ่งว่าถ้า probability การเดาถูก = 0.20 probability ของการเดาผิดจะ = 0.10+0.10 =0.20 เช่นกัน
นั่นคือต่างก็เท่ากับ 50% ดังนั้นถ้าเพียบกับการดู probability เฉพาะแต่ที่ผลรวมของ B อย่างเดียวแล้ว การทราบข่าวสารเพิ่มขึ้น (เช่นมาจากช่วง A 1 เป็นต้น) ย่อมทำให้การทำนายผิดพลาดลงได้ นั่นคือลดลงไป = 60 – 50 =10 %
ความผิดพลาดที่ลดลงไปอันเนื่องมาจากการทราบข่าวสารเพิ่มขึ้น (ข่าวสารซึ่งมาจากตัวแปรอิสระ) เปรียบเทียบกับความผิดพลาดที่เกิดจากการทำนายจากผลรวมอย่างเดียวโดยไม่ทราบข่าวสารอะไรเลย เราเรียกอัตราส่วนนี้ว่า Proportional Reduction in Error (PRE) ซึ่งเป็นรูปหนึ่งของการวัดความสัมพันธ์ระหว่างตัวแปร การที่ความผิดพลาดในการทำนายลดลง แสดงว่าตัวแปรตัวหนึ่งอธิบายตัวแปรอีกตัวแปรอีกตัวหนึ่งได้ ตัวแปรทั้งสองจึงมีความสัมพันธ์กัน แบบฟอร์ม (สูตร) ในการหาค่า PRE โดยทั่วๆไปคือ
( E 1 – E 2 )/ E 1
E 1 คือ ความผิดพลาดเมื่อไม่ทราบข่าวสารจากตัวแปรอิสระ คือ ดูจากผลรวมตัวแปรตาม แต่เพียงอย่างเดียว
E 2 คือ ความผิดพลาดที่ยังไม่เกิดขึ้น แม้มีข่าวสารเพิ่มขึ้นมาจากตัวแปรอิสระ
โดยทั่วๆไป สถิติแบบ PRE มักจะหาค่าโดยอาศัยแบบฟอร์มของรูปสูตรดังข้างบน เพียงแต่ว่าการหาค่าความผิดพลาดทั้ง E 1 และ E 2 แตกต่างกันไปตามแต่นักสถิติผู้คิดค้นนั้นๆ จะคิดออกมาได้
|
