| การทดสอบของฟิชเชอร์(The Fisher exact probability test)
การทดสอบนี้เหมาะที่จะใช้วิเคราะห์ ข้อมูลที่มีขนาดเล็ก เพื่อทดสอบว่าประชากรทั้ง 2 แตกต่างกันอย่างมีนัยสำคัญหรือไม่ในค่าสัดส่วนของเหตุการณ์ที่สนใจ เมื่อข้อมูลที่นำมาวิเคราะห์เป็นแบบนามบัญญัติหรือแบบเรียงลำดับ
ข้อมูล จะประกอบด้วยตัวอย่าง 2 ชุดที่เป็นอิสระต่อกัน และตัวอย่างทั้ง 2 นั้นจะประกอบด้วยลักษณะใดลักษณะหนึ่ง ซึ่งแยกจากกันเด็ดขาด สามารถจัดข้อมูลลงในตาราง 2x2 ดังนี้
|
กลุ่มที่ 1 |
กลุ่มที่ 2 |
ผลรวม |
ลักษณะ + |
A |
B |
A+B |
ลักษณะ - |
C |
D |
C+D |
ผลรวม |
A+C |
B+D |
N |
กลุ่มที่ 1 และ 2 หมายถึงตัวอย่าง 2 กลุ่มทีเป็นอิสระกัน ซึ่งอาจจะเป็นกลุ่มทดลองกับกลุ่มควบคุม , เพศชายกับเพศหญิง , กลุ่มคนที่มีงานทำกับกลุ่มคนที่ว่างงาน หรือกลุ่มคนที่นิยมพรรคการเมือง ก กับกลุ่มที่นิยมพรรคการเมือง ข
ส่วนทางแถวนอนที่มีเครื่องหมาย – และ + นั้นหมายถึง การแบ่งกลุ่มออกเป็น 2 ลักษณะใดๆเช่น การสอบตกและสอบผ่าน , การเห็นด้วยและไม่เห็นด้วย , มีค่าสูงกว่ามัธยฐานและค่าต่ำกว่ามัธยฐาน
วิธีการรวบรวมข้อมูล คือการสำรวจตัวอย่างขนาด n ซึ่งจะเป็นกลุ่มที 1 ขนาด n 1 ( หรือ = A+C) และกลุ่มที่ 2 ขนาด n 2 ( หรือ = B+D) หาจำนวนที่ตกในแต่ละลักษณะในแต่ละกลุ่ม เช่นในกลุ่มที่ 2 มีจำนวนตัวอย่าง = B ที่มีลักษณะ + เป็นต้น
การทดสอบด้วยวิธีนี้ สามารถใช้ได้ดีกับตัวอย่างขนาดเล็กคือ n < 20
ข้อกำหนดเบื้องต้น
• ข้อมูลประกอบด้วยตัวอย่างสุ่มขนาด n 1 จากประชากรที่ 1 และตัวอย่างสุ่มขนาด n 2 จากประชากรที่ 2 และให้ N = n 1 + n 2
• ตัวอย่างทั้ง 2 เป็นอิสระต่อกันทั้งภายในกลุ่มและระหว่างกลุ่ม
• แต่ละตัวอย่างจะถูกจัดให้เป็นลักษณะ + หรือ – ลักษณะใดลักษณะหนึ่งเท่านั้น ดังนั้นมาตราวัดที่จะใช้ได้สำหรับการทดสอบนี้คือ นามบัญญัติหรือเรียงลำดับ
สมมติฐาน อาจจะเป็นการทดสอบสองหางหรือหางเดียวก็ได้ ดังนี้
ถ้าให้ P 1 และ P 2 คือค่าสัดส่วนของลักษณะ +( หรือ –) ของประชากรที่ 1 และ 2 ตามลำดับ
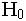 : ค่าสัดส่วนของลักษณะ +( หรือ –) มีค่าเท่ากันในประชากรทั้ง 2 : ค่าสัดส่วนของลักษณะ +( หรือ –) มีค่าเท่ากันในประชากรทั้ง 2
 : ค่าสัดส่วนของลักษณะ +( หรือ –) มีค่าแตกต่างในประชากรทั้ง 2 : ค่าสัดส่วนของลักษณะ +( หรือ –) มีค่าแตกต่างในประชากรทั้ง 2
หรือ 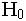 : P 1 = P 2 : P 1 = P 2  : P 1 : P 1 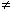 P 2 P 2
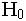 : ค่าสัดส่วนของลักษณะ +( หรือ –) ในประชากรที่ 1 ? ค่าสัดส่วนของลักษณะ +( หรือ –) ในประชากรที่ 2 : ค่าสัดส่วนของลักษณะ +( หรือ –) ในประชากรที่ 1 ? ค่าสัดส่วนของลักษณะ +( หรือ –) ในประชากรที่ 2
H 1 : ค่าสัดส่วนของลักษณะ +( หรือ –) ในประชากรที่ 1 > ค่าสัดส่วนของลักษณะ +( หรือ –) ในประชากรที่ 2
หรือ 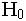 : P 1 <= P 2 : P 1 <= P 2  : P 1 > P 2 : P 1 > P 2
วิธีการ สามารถหาค่าความน่าจะเป็น ( exact probability ) ที่จะเกิดความถี่ที่ได้จากการสังเกต ( observed frequency ) และมีค่าใดๆ ตกอยู่ในตาราง 2x2 เมื่อกำหนดให้ผลรวมมาร์จินัลมีค่าคงที่ ( fixed marginal totals ) ได้ โดยหาจากฟังก์ชันการแจกแจงแบบไฮเปอร์จิออเมตริก ( hyper geometric distribution ) ดังนี้

จะพบว่าสูตรนี้คือ ค่าอัตราส่วนของผลคูณของแฟคตอเรียลของผลรวมทางแถวนอนและแถวตั้งต่อความถี่ของแต่ละเซลและความถี่ทั้งหมด
ตัวอย่างเช่น สมมติได้ข้อมูลขนาด N = 19 และจัดลงในตารง 2x2 ได้ดังนี้
ตารางที่ 1
|
กลุ่มที่ 1 |
กลุ่มที่ 2 |
ผลรวม |
ลักษณะ + |
0 |
5 |
5 |
ลักษณะ - |
10 |
4 |
14 |
ผลรวม |
10 |
9 |
19 |
จะได้ความน่าจะเป็นที่ 19 หน่วยตัวอย่างนี้ ตกอยู่ใน 4 เซลของตารง 2x2 ดังที่เป็นอยู่นี้คือ

ถ้าสังเกตจะพบว่าตัวอย่างข้างต้น เป็นกรณีที่มีความถี่ = 0 ในเซลใดเซลหนึ่งแต่เมื่อกำหนดให้ผลรวมมาร์จินัลมีค่าคงที่ ดังนั้น จึงสามารถจัดความถี่ลงในตาราง 2x2 ได้หลายแบบ เช่นตัวอย่างต่อไปนี้
ตารางที่ 2
|
กลุ่มที่ 1 |
กลุ่มที่ 2 |
ผลรวม |
ลักษณะ + |
6 |
1 |
7 |
ลักษณะ - |
1 |
4 |
5 |
ผลรวม |
7 |
5 |
12 |
ซึ่งจะได้ค่า

หรือสามารถจัดความถี่ลงในตาราง 2x2 ได้อีกแบบหนึ่ง โดยที่ผลรวมมาร์จินัลคงที่ดังตาราง 2.1
ตารางที่ 2.1
|
กลุ่มที่ 1 |
กลุ่มที่ 2 |
ผลรวม |
ลักษณะ + |
7 |
0 |
7 |
ลักษณะ - |
0 |
5 |
5 |
ผลรวม |
7 |
5 |
12 |

ดังนั้นในตัวอย่างนี้ ความน่าจะเป็นที่จะได้ 12 ตัวอย่าง ตกอยู่ในเซลต่างๆของตาราง 2x2 เมื่อผลรวมมาร์จินัลคงที่= 0.04399+0.00126 = 0.04529ซึ่งคือค่า P – value ใช้ช่วยตัดสินใจว่าข้อมูลจากตารางที่ 2 จะทำให้สามารถปฏิเสธ 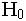 เพื่อยอมรับ เพื่อยอมรับ  ( แบบทางเดียว ) ได้หรือไม่ ( แบบทางเดียว ) ได้หรือไม่
การปรับความถี่ในเซลต่างๆทั้ง 4 ในตาราง 2x2 นั้น มีเกณฑ์อย่างไร ให้ลองพิจารณาตัวอย่างต่อไปนี้ จะเข้าใจง่ายขึ้น
ตัวอย่างที่ 3.2 ถ้าสุ่มตัวอย่างขนาด 7 และ 8 จากประชากรที่ 1 และ 2 ตามลำดับ โดยที่ประชากรทั้ง 2 เป็นอิสระต่อกัน เมื่อทำการจำแนกว่าแต่ละตัวอย่างมีคุณลักษณะ + หรือ – อย่างไร ได้ข้อมูลตัวอย่างดังนี้
|
กลุ่มที่ 1 |
กลุ่มที่ 2 |
ผลรวม |
ลักษณะ + |
5 |
1 |
6 |
ลักษณะ - |
2 |
7 |
9 |
ผลรวม |
7 |
8 |
15 |

ดังนั้นค่า P – value ที่จะหาจากฟังก์ชันการแจกแจงไฮเปอร์จิออเมตริกนั้นต้องหาในกรณีที่เป็นตัวอย่างจริง และกรณีที่มีค่ามากกว่าตัวอย่างจริง( extreme or more extreme ) ดังนี้
จากตัวอย่าง




หมายเหตุ ในการทดสอบสองหาง จำนวน more extreme ทางมากกว่าและน้อยกว่ามักจะเท่ากันเพื่อให้เป็นการทดสอบสมมติฐานแบบที่มีอาณาเขตวิกฤตปลายหางซ้ายขวาใกล้เคียงกัน หรือช่วงการยอมรับจะอยู่กลางของโค้งการแจกแจง
ค่าในแถวตั้งที่ 5 , 6 และ 7 จะได้กล่าวถึงในการใช้ตารางสำเร็จรูปดังต่อไปนี้ วิธีการดังกล่าวข้างต้นแม้จะมีผลดีในแง่ที่สามารถคำนวณหาค่าความน่าจะเป็นที่แท้จริงได้ถูกต้อง แต่จะพบว่าในทางปฏิบัติจะเสียเวลา และน่าเบื่อมาก จึงได้มีผู้สร้างตารางสำเร็จรูป เมื่อมีข้อจำกัดว่าขนาดตัวอย่าง n 1 +n 2 = N ? 15 วิธีการใช้ตารางอธิบายได้ดังนี้
1 . ให้พิจารณาค่าผลรวมทางแถวนอนและแถวตั้งของตาราง 2x2 จากตัวอย่างที่สังเกตได้จริง ให้
S 1 = ค่าผลรวมมาร์จินัลที่มีค่าน้อยที่สุด (อาจจะเป็นแถวนอนหรือแถวตั้งก็ได้)
S 2 = ค่าผลรวมมาร์จินัลที่มีค่าน้อยอันดับที่ 2 จากแถวที่ตรงกันข้ามกับ S 1 เสมอ เช่น
S 1 = ผลรวมทางแนวนอน S 2 จะต้องเป็นผลรวมแนวตั้ง เช่น

2. ให้ X = ความถี่ที่สังเกตได้จริงจากตัวอย่างขนาด N ซึ่งอยู่ในเซลที่ S 1 และ S 2 ตัดกัน (ดังรูปตารางในข้อ 1)
3. ในแต่ละค่าของ N, S 1 , S 2 , X ในตารางการแจกแจงของสถิติฟิชเชอร์ จะมีแถวตั้ง 3 แถวใหญ่
แถวที่ 1 obs. คือค่า p ที่ได้จาก  : แบบหางเดียว : แบบหางเดียว
แถวที่ 2 other คือค่า p ที่ได้จากการจัดตาราง 2x2 ในทิศทางตรงข้ามกับ  : แบบหางเดียว : แบบหางเดียว
แถวที่ 3 Total คือค่า p ที่ได้จาก  แบบสองหาง แบบสองหาง
ตัวอย่างที่ 3.4 จากอาสาสมัคร 21คน เลือกมา 11 คนอย่างสุ่มแล้วให้ทานยาซึ่งสามารถดูดซึมแอลกอฮอล์ และ 10 คน ที่เหลือไม่ให้ทานยาใดๆ หลังจากนั้นแต่ละคนจะได้ดื่มเหล้า หนึ่งชั่วโมงหลังจากนั้นได้ทดสอบลมหายใจ ( Breathalyser test ) ซึ่งจะแสดงว่ามีแอลกอฮอล์ในกระแสเลือดหรือไม่ ได้ผลดังตาราง



<<หน้าที่แล้ว หน้าต่อไป>> |
