การวัดความสอดคล้องกันจะแตกต่างจากการวัดความสัมพันธ์ ( Measure of association ) โดยจะเป็นการศึกษาว่าผู้ประเมิน 2 คน (หรือ k คน) มีความเห็นในทิศทางเดียวกันหรือไม่ในการจัดกลุ่มตัวอย่างลงในกลุ่มต่างๆ (หรือลำดับที่ต่างๆ) ความสอดคล้องกันสูงจะหมายถึงมีความสัมพันธ์กันสูงด้วย แต่ความสัมพันธ์ที่สูงอาจจะไม่มีความสอดคล้องกัน เช่น ถ้าผู้ประเมิน X ประเมินในหน่วยตัวอย่างในระดับที่สูงกว่าผู้ประเมิน Y ในทุกหน่วยตัวอย่าง นั่นคือ ความสอดคล้องกันต่ำ แต่มีความสัมพันธ์กันสูง
จะกล่าวถึงสถิติที่ใช้วัดความสอดคล้องกัน 3 ค่าดังต่อไปนี้ Kendall coefficial of concordance , w
ใช้เพื่อวัดความสัมพันธ์ของชุดข้อมูล k ชุดที่มีลักษณะลำดับที่ (k sets of ranking) มีประโยชน์เพื่อใช้ในการศึกษาถึงความสอดคล้องกันของผู้ตัดสิน k คน (interjudge) หรือแบบทดสอบ k ชุด ( interest reliability) รวมทั้งสามารถนำนำไปประยุกต์เกี่ยวกับการจัดกลุ่มของตัวแปรต่างๆ (cluster of variable)
วิธีการ
ให้จัดข้อมูลลงในตาราง ชนิด k x n โดยที่แถวนอน จะหมายถึง k ตัวแปร(หรือผู้ตัดสิน k คน , แบบทดสอบ k แบบ) ที่มีค่าข้อมูลเป็นลำดับที่ 1- N เมื่อ N หมายถึง หน่วยทดสอบ(หรือแบบทดสอบ) ที่ถูกจัดลำดับที่ เช่นผู้บริหาร บริษัทแห่งหนึ่ง 3 ท่าน สัมภาษณ์ผู้สมัครเข้าทำงาน 6 คน สมมติได้ค่าลำดับที่ของผู้สมัครทั้ง 6 ดังตารางต่อไปนี้
|
ผู้สมัครคนที่ |
ผู้บริหาร |
a |
b |
c |
d |
e |
f |
x |
1 |
6 |
3 |
2 |
5 |
4 |
y |
1 |
5 |
6 |
4 |
2 |
3 |
z |
6 |
3 |
2 |
5 |
4 |
1 |
ผลรวมลำดับที่ Ri |
8 |
14 |
11 |
11 |
11 |
8 |
ค่าเฉลี่ยลำดับที่ 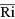 |
2.67 |
4.67 |
3.67 |
3.67 |
3.67 |
2.67 |
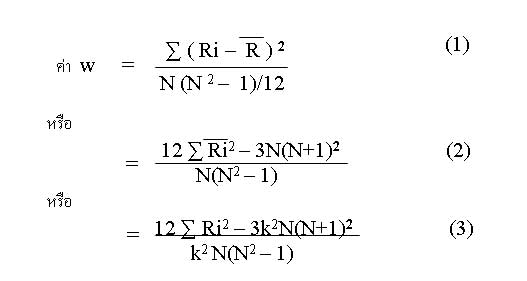
จากตัวอย่างข้างต้น ถ้าใช้สูตรที่ 3 จะได้ค่า w ดังนี้
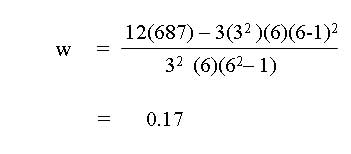
ค่า w จะมีค่าในช่วง ( 0-1 ) จะไม่มีค่าเป็นลบ เนื่องจากในกรณีที่มี k ชุดของข้อมูล จะไม่มีชุดข้อมูลใดที่จะสัมพันธ์ทิศทางตรงกันข้ามอย่างสมบูรณ์ได้
การทดสอบนัยสำคัญของ w โดยตั้ง
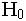 : ไม่มีความสัมพันธ์ระหว่าง k ตัวแปร : ไม่มีความสัมพันธ์ระหว่าง k ตัวแปร
 : มีความสัมพันธ์ระหว่าง k ตัวแปร : มีความสัมพันธ์ระหว่าง k ตัวแปร
กรณีตัวอย่างเล็ก เมื่อ k = 3 ถึง 20 และ N = 3 ถึง 7 ใช้ตารางค่าวิกฤติของการแจกแจงของตัว
สถิติ w โดยตรง โดยจะปฏิเสธ 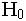 เมื่อค่า w จากตัวอย่างมีค่ามากกว่าหรือ เท่ากับค่าวิกฤต ที่ระดับนัยสำคัญ 0.01 หรือ 0.05 เมื่อค่า w จากตัวอย่างมีค่ามากกว่าหรือ เท่ากับค่าวิกฤต ที่ระดับนัยสำคัญ 0.01 หรือ 0.05
กรณีตัวอย่างใหญ่ เมื่อ N >7 จะใช้การแจกแจงไคสแควร์ ด้วยสูตรดังนี้
 = k (N – 1 ) w = k (N – 1 ) w
ถ้าค่า  จากตัวอย่าง มีค่ามากกว่าหรือเท่ากับค่าวิกฤต จากตัวอย่าง มีค่ามากกว่าหรือเท่ากับค่าวิกฤต  ที่องศาความเป็นอิสระ = N – 1 จะปฏิเสธที่ระดับนัยสำคัญหนึ่ง ที่องศาความเป็นอิสระ = N – 1 จะปฏิเสธที่ระดับนัยสำคัญหนึ่ง
ตัวอย่างที่ 1 จากตัวอย่างข้างต้น ซึ่งได้ w = 0.17 เมื่อ k = 3 N= 6 ใช้ตารางค่าวิกฤตของ w ที่ a =0.05 ได้ค่าวิกฤต w =0.660 ดังนั้น สรุปว่า w ไม่ตกในอาณาเขตวิกฤตจึงยอมรับ 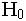 นั่นคือ การให้ลำดับที่ของผู้บริหารทั้ง 3 เป็นอิสระกัน นั่นคือ การให้ลำดับที่ของผู้บริหารทั้ง 3 เป็นอิสระกัน โปรแกรมคำนวณ
_____________________________________________
Kendall coefficient of agreement u for paired comparison or ranking ในหัวข้อที่ผ่านมา การให้ผู้ตัดสิน(ตัวแปร k ตัว) ให้ลำดับที่ 1- N อาจจะทำได้ยากเมื่อ N ใหญ่ ดังนั้นแทนที่จะให้ลำดับ 1- N อาจให้ผู้ตัดสินลำดับที่ในคู่ของหน่วยทดลอง และให้ผู้ตัดสินเปรียบเทียบในคู่นี่ว่า หน่วยทดลองใดที่ดีกว่า
วิธีการ จากหน่วยทดลองขนาด N ให้จับคู่เพื่อเปรียบเทียบ ซึ่งจะได้จำนวนคู่ทั้งหมด N C 2 คู่ เช่นมี N=4 ด้วยหน่วยทดลอง a,b,c,d สามารถ จับคู่ได้ 4 C 2 คู่ = 6 คู่ และให้เปรียบเทียบภายในคู่ สมมติได้ข้อมูลดังนี้
คู่ หน่วยทดลองที่ถูกเลือก (Preference)
(a,b) a
(a,c) a
(a,d) d
(b,c) b
(b,d) d
(c,d) d
และนำข้อมูลที่ได้มาจัดลงตารางที่เรียกว่า Preference matrix ซึ่งจะสรุปถึงจำนวนครั้งที่แต่ละหน่วยทดลองถูกเลือก (หรือมีลำดับที่นำหน้า) เมื่อเทียบกำหน่วยทดลองอื่น โดยแสดงถึงจำนวนครั้งที่ตัวแปรแถวนอนถูกเลือกเมื่อเปรียบเทียบกับตัวแปรตามแนวตั้งจากตัวอย่างข้างต้นจะได้ดังนี้
Preference matrix
|
a |
b |
c |
d |
a |
- |
1 |
1 |
- |
b |
- |
- |
1 |
- |
c |
- |
- |
- |
- |
d |
1 |
1 |
1 |
- |
จะพบว่าความถี่ในแนวทะแยงมุมจะไม่มีค่าเสมอของผู้ตัดสิน k คน ถ้ามีการให้ลำดับที่สอดค้ลองกันอย่างสมบูรณ์ในแต่ละคู่ของหน่วยทดลองจะมี N(N-1)/2 เซลล์ที่ได้ความถี่ = k และที่เหลือ N(N-r)/2 เซล จะมีความถี่เป็น 0
จากตัวอย่างเดิมที่ผ่านมา ถ้านำข้อมูลมาสร้าง ตาราง Preference matrix จะได้ดังนี้
|
ผู้สมัครคนที่ |
ผู้บริหาร |
a |
b |
c |
d |
e |
f |
X |
1 |
6 |
3 |
2 |
5 |
4 |
Y |
1 |
5 |
6 |
4 |
2 |
3 |
Z |
6 |
3 |
2 |
5 |
4 |
1 |
Preference matrix
|
a |
b |
c |
d |
e |
f |
a |
- |
2 |
2 |
2 |
2 |
2 |
b |
1 |
- |
1 |
1 |
1 |
0 |
c |
1 |
2 |
- |
1 |
2 |
1 |
d |
1 |
2 |
2 |
- |
1 |
1 |
e |
1 |
2 |
1 |
2 |
- |
1 |
f |
1 |
3 |
2 |
2 |
2 |
- |


จากตัวอย่างข้างต้นสรุปได้ว่า ผู้บริหาร 3 คน เมื่อให้ลำดับที่ภายในคู่ จะมีความเห็นที่ไม่สอดคล้องกันค่อนข้างสูง (เนื่องจากค่าต่ำสุด = -1/3 = -0.33 ) การทดสอบนัยสำคัญของค่า U
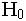 : : 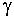 = 0 เมื่อ = 0 เมื่อ 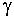 = ค่าพารามิเตอร์ของค่าสถิติ U = ค่าพารามิเตอร์ของค่าสถิติ U
 : : 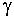 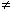 0 0
หรือ
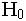 : ไม่มีความสอดคล้องกันของคำตัดสินของผู้ตัดสินเมื่อเปรียบเทียบทีละคู่ : ไม่มีความสอดคล้องกันของคำตัดสินของผู้ตัดสินเมื่อเปรียบเทียบทีละคู่
 : มีความสอดคล้องกันของคำตัดสินของผู้ตัดสินเมื่อเปรียบเทียบทีละคู่ : มีความสอดคล้องกันของคำตัดสินของผู้ตัดสินเมื่อเปรียบเทียบทีละคู่
เมื่อจำนวนผู้ตัดสิน = 6 (k = 6) และมีหน่วยทดลอง = 8 (N = 8) ใช้การแจกแจงของสถิติ U ช่วยตัดสินใจ โดยหาค่าพื้นที่ปลายขวาของโค้งการแจกแจงของ U ของค่า U ที่คำนวณได้ จากตัวอย่าง ซึ่งจะคือค่า p (p-value) พิจารณาค่าว่าค่า p ใหญ่พอหรือไม่ โดยทั่วไปถ้าใหญ่กว่า 0.05 จะยอมรับ 
ในกรณีที่ k และ N เป็นกรณีอื่นๆ สามารถใช้การแจกแจงของ Chi'square ประมาณได้ดังสูตร
โปรแกรมคำนวณ
_____________________________________________
หน้าต่อไป>> |
